在机器学习的世界里,一个模型宣称拥有 98% 的准确率,听起来确实很棒,对吗?但现实情况可能比这复杂得多。尤其当你处理那些“罕见事件”,比如欺诈交易或者疾病诊断时,仅仅看准确率可能会给我们一种虚假的安全感。
这时候,精准率(Precision)和召回率(Recall)这两个指标就派上用场了。它们不仅仅告诉我们模型“对”了多少次,更重要的是,它们能揭示模型错在了哪里,以及错得多严重。这篇文章,我准备和大家一起深入探讨这两个至关重要的指标,看看它们是如何超越简单的准确率,帮我们更全面地评估模型表现的。
如果你对分类模型评估有兴趣,想从理论走向实践,那么继续读下去,肯定会有收获。
为什么只看准确率远远不够?
大多数时候,我们习惯用准确率(Accuracy)来衡量一个统计或机器学习模型预测标签的好坏。它的计算方法很简单:正确预测的实例数除以总观测数。直观上看,如果一个模型总是能以高准确率识别正确标签,那它看起来就运行得挺好。
然而,当数据集出现不平衡时,准确率就会变得很有“欺骗性”。所谓不平衡数据集,指的是其中一个类别(比如“正常交易”)的样本量远大于另一个类别(比如“欺诈交易”)。在欺诈检测或疾病诊断这类场景里,不平衡数据很常见。
比方说,一个模型在欺诈检测任务中达到了 98% 的准确率。初听上去,这个数字相当惊人。但是,如果整个数据集中欺诈交易只占 2% 呢?在这种情况下,模型即使每次都简单地预测“不是欺诈”,它依然能得到 98% 的准确率。但结果是,它一个欺诈案例也没抓到,这显然不是我们想要的效果。
很明显,在这些情境下,我们需要更精细的衡量指标。而精准率和召回率,就是我们常常会用到的两个好帮手。
精准率与召回率,到底是什么?
简单来说,我们可以这样理解:
- 精准率 (Precision) —— 衡量“预测的质量”:它回答的是,在模型预测为正例的所有样本中,有多少比例是真的正例。换句话说,如果模型说“这是欺诈”,那它是不是真的欺诈?
- 召回率 (Recall) —— 衡量“捕获的全面性”:它关注的是,在所有实际的正例中,模型成功捕获了多少比例。也就是说,模型有没有把所有的欺诈案例都找出来,还是漏掉了一些?
要搞清楚如何计算这两个指标,我们首先得认识混淆矩阵里的一些基本术语。
真正例、假正例与负例们
想象一下,一家信用卡公司使用机器学习模型来检测欺诈交易。假设在 10,000 笔交易样本中,有 9,800 笔是合法交易,200 笔是欺诈交易。
为了评估模型的有效性,我们需要把“欺诈”或“非欺诈”中的一个指定为正例,另一个为负例。既然我们更关注欺诈案例,那就把“欺诈”标记为“正例”。(这当然不是说欺诈是道德上的“正”,这里“正”只是代表我们感兴趣的那个类别。)
当模型运行后,如果交易的风险评分超过某个概率阈值(比如 70%),就被认为是欺诈。然后,我们将模型预测为欺诈的案例与实际为欺诈的案例进行比较。
为了清晰地整理这些数据,我们引入以下术语:
- 真正例 (True Positives, TP):160 笔欺诈交易被模型正确地预测为欺诈。
- 真负例 (True Negatives, TN):9500 笔合法交易被模型正确地识别为非欺诈。
- 假正例 (False Positives, FP):300 笔合法交易被模型错误地标记为欺诈。(也叫误报)
- 假负例 (False Negatives, FN):40 笔欺诈交易被模型错误地标记为非欺诈。(也叫漏报)
这里的第二个字母(P 或 N)表示模型的预测是正例还是负例,而第一个字母(T 或 F)则表示这个预测是“真”(正确)还是“假”(错误)。
一个“假正例”意味着系统预测它是正例,但它实际上是负例。比如,一个“假负例”就是系统预测它是负例,但它实际上是正例。
混淆矩阵
所有这些信息通常都会汇总在一个叫做“混淆矩阵”(Confusion Matrix)的表格里。混淆矩阵能帮我们清晰地看到模型在哪些地方把预测结果与实际结果“搞混”了(即 FN, FP)。
以我们的例子来说,混淆矩阵是这样子的:
| 实际欺诈 (实际正例) | 实际合法 (实际负例) | |
|---|---|---|
| 预测欺诈 (预测正例) | 160 (TP) | 300 (FP) |
| 预测合法 (预测负例) | 40 (FN) | 9500 (TN) |
现在,我们再看看行和列的总计:
| 实际欺诈 (实际正例) | 实际合法 (实际负例) | ||
|---|---|---|---|
| 预测欺诈 (预测正例) | 160 (TP) | 300 (FP) | 460 (TP + FP) 总预测正例数 |
| 预测合法 (预测负例) | 40 (FN) | 9500 (TN) | 9540 (FN + TN) 总预测负例数 |
| 200 (TP + FN) 总实际正例数 | 9800 (FP + TN) 总实际负例数 | 10,000 (总样本量) |
这些总计代表了什么呢?
- 第一行总计 (460) 表示模型预测为欺诈的总案例数 (TP + FP)。
- 第二行总计 (9,540) 表示模型预测为合法的总案例数 (FN + TN)。
- 第一列总计 (200) 表示实际欺诈的总案例数 (TP + FN)。
- 第二列总计 (9,800) 表示实际合法的总案例数 (FP + TN)。
- 总计 (10,000) 就是我们样本的总大小。
什么是精准率?
精准率 (Precision) 衡量的是你正向预测的“质量”。它告诉我们,在所有模型预测为正例的案例中,有多少比例是真的正例。
一个高精准度的模型意味着很少有虚假警报。如果模型说某件事是真的,那它很可能就是真的。比如,在一个在线游戏中,如果一个作弊检测系统封禁了某个玩家,这个封禁的理由必须是真实的。太多的误封(假正例)会疏远正常玩家,并导致负面评价。
用前面定义的术语来说,精准率等于真正例数除以预测为正例的总数。
$$ \text{Precision} = \frac{\text{TP}}{\text{TP} + \text{FP}} $$
在我们上面的例子中,精准率是 $160 / 460 \approx 34.8%$。
什么是召回率?
召回率 (Recall) 衡量的是模型的“覆盖面”。它显示了在所有实际的正例中,有多少比例被模型成功识别了出来。它的定义是真正例数除以实际正例的总数。
$$ \text{Recall} = \frac{\text{TP}}{\text{TP} + \text{FN}} $$
想象一下癌症早期筛查。在这种情况下,是宁可多报(过度诊断)好,还是漏报(诊断不足)好呢?我想大多数人都会同意前者。
对于早期筛查来说,收到一个假警报确实会让人震惊,但如果实际患癌却被告知没有,这可能是灾难性的,因为患者可能会因此错过潜在的救命治疗。
在我们的例子中,召回率是 $160 / 200 = 80%$。
精准率与召回率的权衡取舍
精准率和召回率之间常常存在一种“此消彼长”的关系。通常情况下,当精准率提高时,召回率往往会下降,反之亦然。
为了理解这一点,我们再回到欺诈检测的例子。
我们最初的模型捕获了大部分欺诈,但也有很多误报(假正例)。假设因为客户投诉增多,管理层决定将决策阈值从 0.7 提高到 0.8。现在,一笔交易必须达到至少 0.8 的评分才会被标记为欺诈,而不是之前的 0.7。
这个调整让模型变得更加“保守”。它预测欺诈的频率降低了。虽然被错误标记为欺诈的交易(假正例)减少了,但代价是更多的真实欺诈案例(假负例)被漏掉了。调整阈值后,假正例的数量从 300 下降到 60,但假负例的数量从 40 上升到 80。
新模型的混淆矩阵变成了这样:
| 实际欺诈 (实际正例) | 实际合法 (实际负例) | ||
|---|---|---|---|
| 预测欺诈 (预测正例) | 120 (TP) | 60 (FP) | 180 (TP + FP) 总预测正例数 |
| 预测合法 (预测负例) | 80 (FN) | 9740 (TN) | 9820 (FN + TN) 总预测负例数 |
| 200 (TP + FN) 总实际正例数 | 9800 (FP + TN) 总实际负例数 | 10,000 (总样本量) |
我们可以看到,在预测为欺诈的 180 笔交易中,有 120 笔确实是欺诈,所以精准率从之前的 34.8% 提升到了 $120 / 180 \approx 66.7%$。
然而,提高精准率的代价是召回率的下降:200 笔实际欺诈交易中,只有 120 笔被模型识别出来,这意味着召回率从最初的 80% 下降到了 $120 / 200 = 60%$。
现在,模型虽然捕获的欺诈案例少了,但当它发出欺诈警报时,我们对这个警报的信心要高得多。这个例子清晰地展示了平衡这两个指标的重要性,这也是我们稍后会讨论的内容。
精准率-召回率曲线
为了直观地展示精准率和召回率之间的这种权衡,数据科学家们会用到精准率-召回率 (Precision-Recall, PR) 曲线。
这条曲线以召回率作为 x 轴,精准率作为 y 轴,描绘了在每个可能的决策阈值(从 0 到 1)下,模型所对应的精准率和召回率。当你降低阈值以捕获更多正例(增加召回率)时,不可避免地也会产生更多的虚假警报(降低精准率)。
一个“完美”的模型会达到右上角(100% 的精准率和召回率),但在实际情况中,你需要在曲线上的某个点进行选择,这个点要符合你具体的业务需求。
在我们欺诈检测的例子中,模型会为每笔交易输出一个欺诈分数。如果交易分数达到或超过阈值,就被标记为欺诈。当我们降低阈值时,我们会得到更多的预测正例,这通常会捕获更多的真正例(提高召回率),但同时也会带来更多的虚假警报(降低精准率)。
让我们看看这在实践中可能是什么样子。假设你的公司每天处理 10,000 笔交易。由于欺诈率估计为 2%,你预计每天有 200 笔欺诈交易。另外,假设欺诈运营团队每天可以审查 200 笔被标记的交易(预测正例)。
你评估了几个阈值,并发现以下结果:
- 阈值 0.9:预测正例 100 笔,精准率 0.8(80 笔实际欺诈,20 笔虚假警报),召回率 0.4(捕获 200 笔欺诈中的 80 笔)。在这种情况下,你的人力资源利用不足,因为你每天只标记 100 笔,但可以审查 200 笔。
- 阈值 0.5:预测正例 500 笔,精准率 0.35(175 笔实际欺诈,325 笔虚假警报),召回率 0.875(捕获 200 笔欺诈中的 175 笔)。在这个阈值下,你超出了处理能力,因为无法审查 500 笔被标记的案例。
- 阈值 0.7:预测正例 200 笔,精准率 0.6(120 笔实际欺诈,80 笔虚假警报),召回率 0.6(捕获 200 笔欺诈中的 120 笔)。这可能就是你会选择的阈值了,因为它既能充分利用团队的处理能力,又能获得一个相对不错的 0.6 召回率。
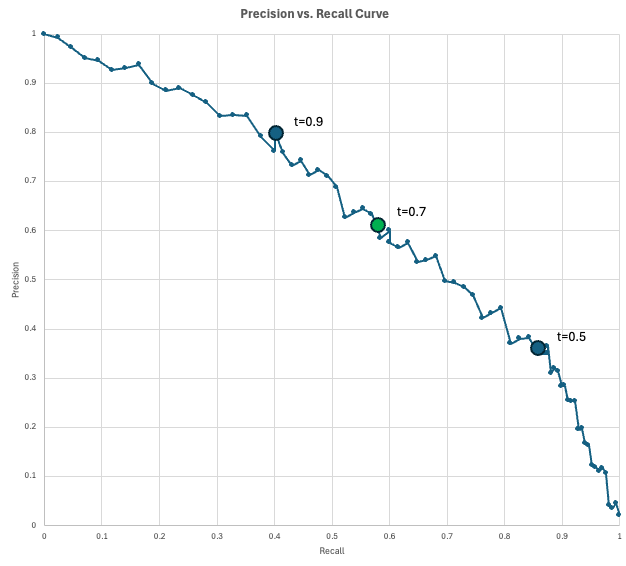
这条曲线清晰地告诉我们,在给定的召回率下,你能“买到”什么样的精准率(反之亦然)。
何时选择精准率,何时选择召回率?
由于精准率和召回率之间的权衡关系,选择哪个指标来优化,真的取决于你具体的应用场景。
何时优先考虑精准率
精准率与假正例之间存在反比关系。所以,一个高精准率的模型意味着它能很好地区分真正例和假正例。这样的模型是值得信任的。
当假正例的成本很高时,就应该优先优化精准率。一些典型的场景包括:
- 不可逆的操作:自动化司法系统或账户封禁系统。如果一个无辜的人被指控,或者一个用户的账户因模型错误(假正例)而被永久删除,这会造成无法弥补的损失。
- 高成本干预:石油钻探或工厂生产线停工。如果基于一个正向预测的行动需要花费数百万美元,你必须确保预测是正确的才能继续。
- 垃圾邮件过滤:电子邮件收件箱。看到一封垃圾邮件(假负例)虽然烦人,但把一封重要的求职信发到垃圾邮件文件夹(假正例)是绝对不能接受的。
何时优先考虑召回率
同样地,召回率与假负例之间也存在反比关系。很多假负例会导致低召回率。因此,一个高召回率的模型能很好地区分真正例和假负例。这样的模型是安全可靠的。
如果避免漏掉一个真实案例比接受一些虚假警报更重要,那么你应该优先考虑召回率而不是精准率。常见的应用场景有:
- 医疗安全:疾病筛查(如癌症或败血症)。漏诊一个病人可能是致命的,而一个假警报只是导致进一步检查,这是可以接受的成本。
- 网络安全:恶意软件检测或网络入侵检测。宁可将一些无害的登录标记为可疑,也不能让一个黑客未经检测就入侵系统。
- 制造质量:缺陷检测。如果将有缺陷的产品出货(假负例)会带来安全责任和声誉损失,那么宁可丢弃一些接近合格的物品,也不要让一个不合格品流向市场。
F1 分数:平衡精准率和召回率的利器
如果你不确定是应该优先优化精准率还是召回率,或者只是想同时兼顾两者,那么 F1 分数会是一个不错的选择。
F1 分数被定义为精准率和召回率的调和平均值,它适用于当你希望在两个指标之间取得平衡时。
$$ \text{F1 Score} = 2 \times \frac{\text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}} $$
如果精准率和召回率相等,那么 F1 分数就等于那个值。但如果其中一个接近于零,F1 分数也会非常低。
在上面我们调整阈值后的例子中,精准率是 66.7%,召回率是 60%。根据公式,我们可以计算出 F1 分数大约是 63.2%:
$$ \text{F1 Score} = 2 \times \frac{0.667 \times 0.60}{0.667 + 0.60} \approx 0.632 $$
下面的表格对比了准确率、精准率、召回率和 F1 分数:
| 指标 | 它回答的问题 | 何时优化此指标 | 示例场景 |
|---|---|---|---|
| 准确率 | “我们整体的正确率是多少?” | 类别分布平衡,且假正例和假负例的成本相似。 | 数字分类。 |
| 精准率 | “在所有预测为正例的案例中,有多少是正确的?” | 当假正例的成本高昂、具有惩罚性或会给客户带来痛苦时。 | 欺诈拦截、用户封禁、侵入性医疗操作。 |
| 召回率 | “在所有实际正例中,我们捕获了多少?” | 假负例是不可接受的。 | 医疗筛查、入侵检测。 |
| F1 分数 | “精准率和召回率的平衡如何?” | 你同时关注正例和虚假警报。 | 不平衡问题的早期模型选择。 |
在 Python 中计算精准率和召回率
在 Python 中计算精准率、召回率和 F1 分数有很多方法。接下来,我将介绍两种常用方法:直接使用公式计算和利用 scikit-learn 库中的专用函数。
使用公式计算精准率和召回率
如果你已经知道了混淆矩阵中的各个数值,那么直接套用上面给出的公式就能轻松计算这些指标。
# 混淆矩阵的数字
TP = 120
FP = 60
FN = 80
TN = 9740
# 公式计算
precision = TP / (TP + FP)
recall = TP / (TP + FN)
f1 = 2 * precision * recall / (precision + recall)
# 输出结果
print(f"{'Precision':<10}{precision:.1%}")
print(f"{'Recall':<10}{recall:.1%}")
print(f"{'F1':<10}{f1:.1%}")
运行这段代码,你会看到:
Precision 66.7%
Recall 60.0%
F1 63.2%
这个输出结果与我们之前的计算是完全一致的。
使用 scikit-learn 计算精准率和召回率
我们也可以利用 scikit-learn 库来直接从原始数据中计算这些指标。在下面的例子中,我们模拟了 y_true(真实标签)和 y_predicted(模型预测标签)。然后,我们使用 precision_score(y_true, y_pred) 方法来计算精准率,召回率和 F1 分数的计算方式也类似。
import numpy as np
from sklearn.metrics import precision_score, recall_score, f1_score
# 模拟数据 (y_true 和 y_pred)
TP, FP, FN, TN = 120, 60, 80, 9740
y_true = np.array(TP * [1] + FP * [0] + FN * [1] + TN * [0]) # 真实标签:1代表正例,0代表负例
y_pred = np.array(TP * [1] + FP * [1] + FN * [0] + TN * [0]) # 预测标签:1代表正例,0代表负例
# 使用 scikit-learn 计算指标
precision = precision_score(y_true, y_pred, zero_division=0) # zero_division=0 避免除以零错误
recall = recall_score(y_true, y_pred, zero_division=0)
f1 = f1_score(y_true, y_pred, zero_division=0)
# 打印对齐的输出
print(f"{'Precision':<10}{precision:.1%}")
print(f"{'Recall':<10}{recall:.1%}")
print(f"{'F1':<10}{f1:.1%}")
运行这段代码,结果同样是:
Precision 66.7%
Recall 60.0%
F1 63.2%
正如我们预料的,这些数字与我们之前的计算结果一致。
总结
虽然准确率是一个不错的起点,但它往往会掩盖模型失败的具体原因。精准率和召回率则能提供更清晰的图像,它们强迫我们去审视误报和漏报之间的权衡。
在我看来,选择正确的评估指标,可不单单是个数学问题;它更是关于你的系统能承受哪种类型错误的实际业务决策。希望大家通过这篇文章,能对这两个指标有一个更深的理解,并在实际项目中,能灵活地运用它们来指导模型优化。
准备好构建你自己的机器学习模型了吗?现在就开始吧!
关于
关注我获取更多资讯

