深入理解 Tanh 激活函数：为何零中心输出至关重要

你有没有遇到过这种情况：神经网络的准确率卡在 60% 上下，怎么调参都没用？你试过调整学习率、增加网络层数、改变 batch size，但训练损失在最初几个 epoch 后就几乎不再下降。这时候，你可能会开始怀疑数据、怀疑模型结构，但问题的根源可能出在一个你没太注意的地方——激活函数。

如果激活函数的输出总是正的，它会把所有更新推向同一个方向，导致网络很难学习到平衡的特征。Tanh（双曲正切函数）就是解决这个问题的一个经典方案。它的输出以零为中心，范围在 -1 到 1 之间，这有助于模型更快地收敛，并让梯度能更顺畅的再网络中流动。

这篇文章会带你彻底搞懂 Tanh，从它的数学原理，到与 Sigmoid、ReLU 的优劣对比，再到 PyTorch 的具体实现。

Tanh 函数究竟是什么？

Tanh 函数，全称 Hyperbolic Tangent，是一个能将任何实数输入映射到 -1 到 1 区间内的函数。它是一条平滑的 “S” 形曲线。

数学公式长这样： $$ \tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} $$

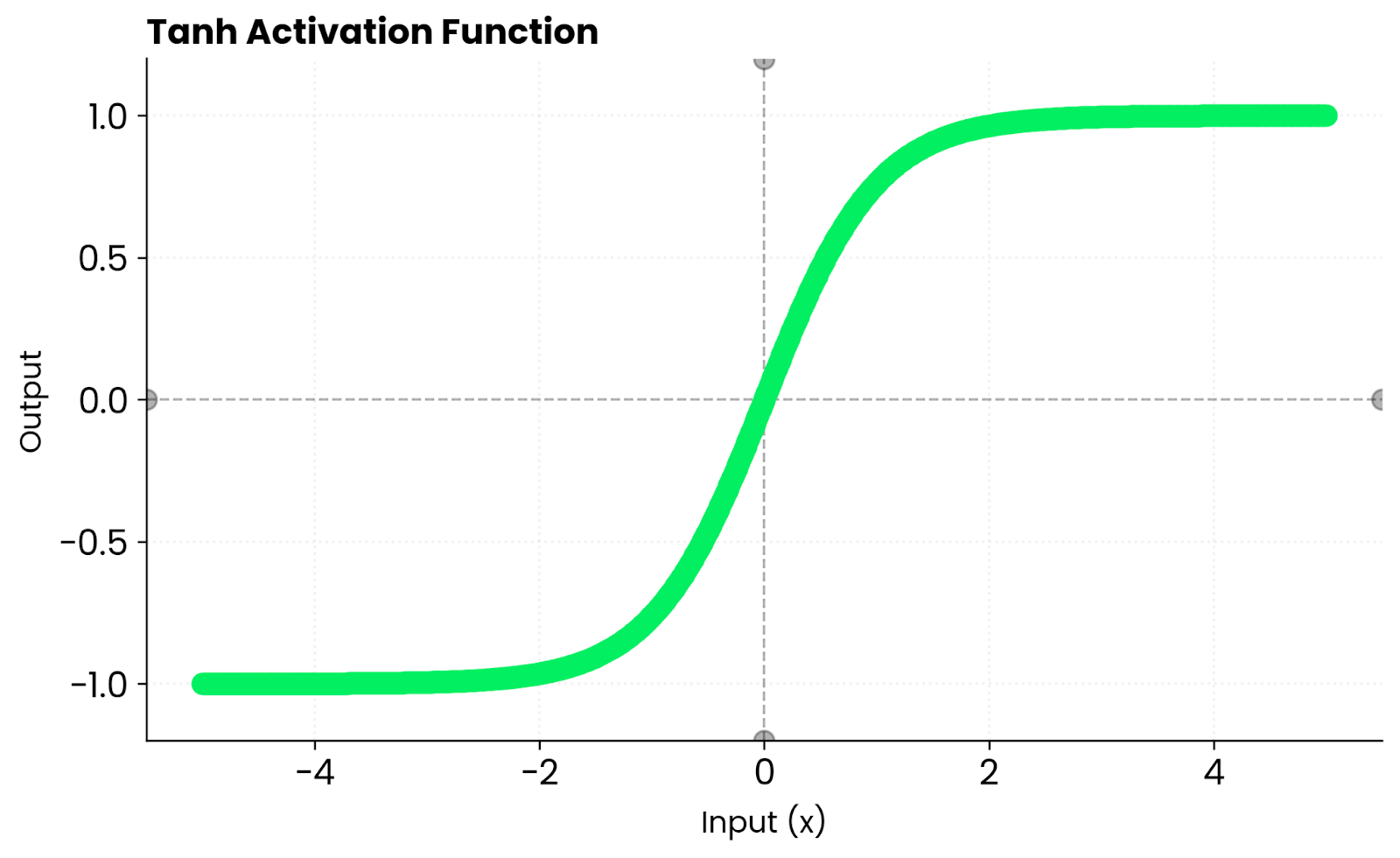
Tanh 函数曲线图

它的行为很直观：

给一个很大的正数，输出就无限接近 1。
给一个很大的负数，输出就无限接近 -1。
输入为 0 时，输出也是 0。

在 0 附近，Tanh 函数近似于一条直线，这意味着梯度可以顺畅地进行反向传播，不会被严重压缩。这与 Sigmoid 函数有本质区别，Sigmoid 的输出范围是 0 到 1，永远是正数。而 Tanh 能输出负值，使得激活值的均值更接近于 0，这种“零中心”的特性在很多场景下能加速模型的收敛。

关键特性：零中心输出与其他数学性质

Tanh 有几个在机器学习中非常重要的数学性质。

零中心输出 (Zero-centered Output)

这是 Tanh 最核心的优势。Sigmoid 函数的输出恒为正，这会导致梯度更新时出现所谓的“偏置偏移”（bias shift），权重更新会朝着一个固定的方向进行，从而减慢收敛速度。

相比之下，Tanh 的输出范围是 [-1, 1]，均值为 0。这意味着激活值的分布更加均衡，权重更新就不会总往一个方向偏，梯度流也因此更稳定，训练起来更快。

平滑且处处可导

Tanh 函数在其定义域内是无限可导的，曲线非常平滑。这对于依赖梯度的优化算法至关重要。不像 ReLU 那样在 x=0 处有个突兀的拐点（导数从0突变为1），Tanh 的平滑特性使得权重更新过程更加稳定和可预测。

有界且稳定

Tanh 的输出被严格限制在 [-1, 1] 之间。这个特性有助于防止“激活值爆炸”的问题，尤其是在一些不稳定的网络结构中，Tanh 能天然地控制住输出的尺度，无需额外的裁剪（clipping）操作。

Tanh 的导数与梯度消失

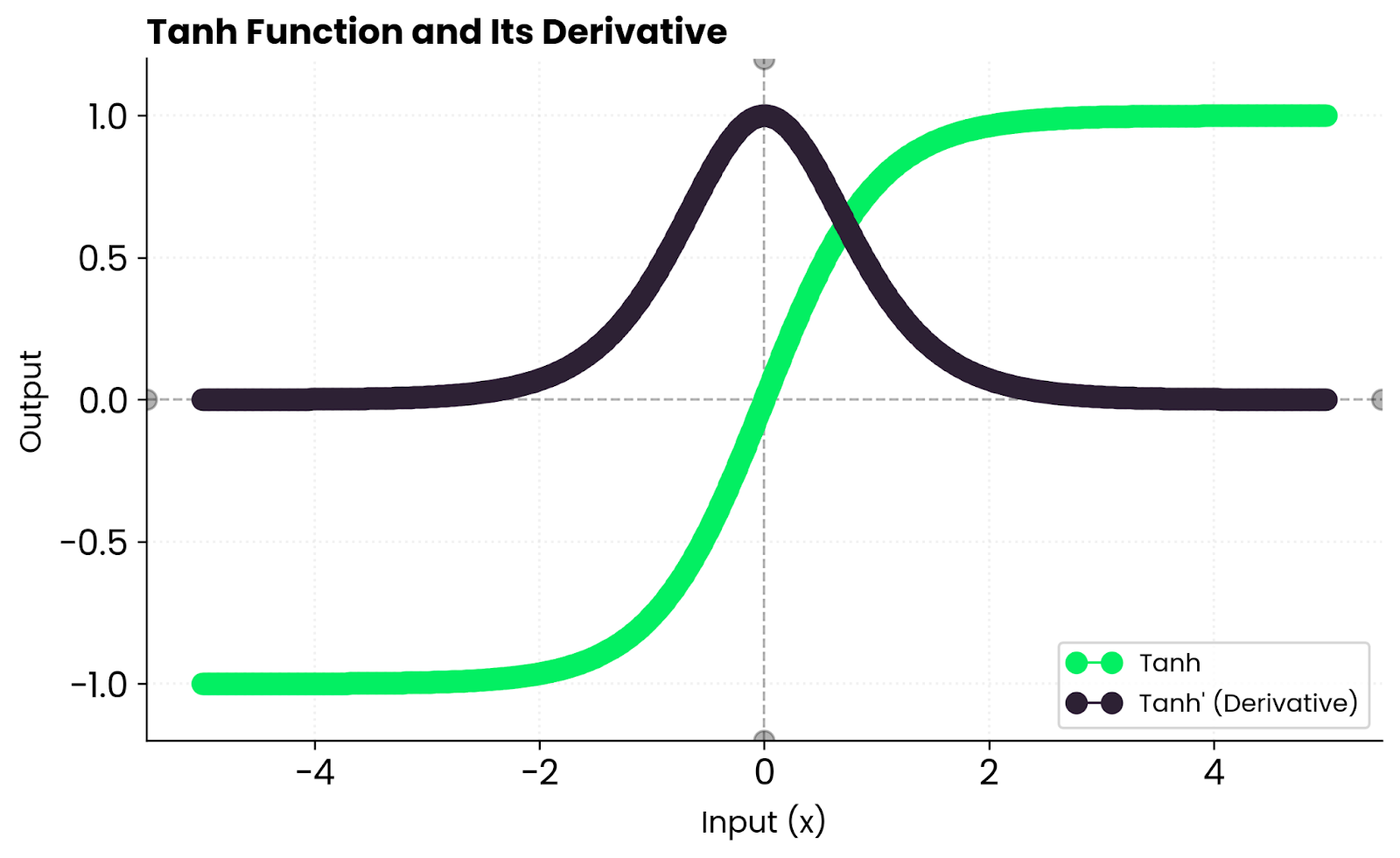
Tanh 的导数也很有特点，公式是： $$ \frac{d}{dx}\tanh(x) = 1 - \tanh^2(x) $$ Tanh 导数曲线图

从导数曲线可以看出，当输入 x 接近 0 时，导数最大（为1），梯度最强。但当 x 变得很大或很小时，tanh(x) 的值会趋近于 1 或 -1，此时导数 1 - tanh²(x) 会趋近于 0。

这就是 Tanh 同样会面临梯度消失（Vanishing Gradients）问题的原因。在深度神经网络中，如果激活值落入饱和区（即绝对值较大的区域），梯度在反向传播时会逐层递减，导致靠近输入层的网络层几乎无法得到有效的更新。

Tanh 与其他激活函数的较量

选择激活函数往往需要在不同特性之间做权衡。

Tanh vs. Sigmoid

实际上，Tanh 可以看作是 Sigmoid 函数的一个缩放和平移版本： $$ \tanh(x) = 2 \cdot \text{sigmoid}(2x) - 1 $$ 它们都是 “S” 形，都会有梯度消失的问题。但 Tanh 的零中心特性，让它在大多数情况下都优于 Sigmoid，收敛速度更快。因此，在需要 “S” 形函数的场景中，Tanh 通常是比 Sigmoid 更好的选择。

Tanh vs. ReLU

ReLU (Rectified Linear Unit) 则是现代神经网络的宠儿。它简单粗暴但极其有交：f(x) = max(0, x)。

优势：ReLU 对正数输入不饱和，计算速度极快，还能通过让部分神经元输出为零来引入稀疏性，从而加速训练。
劣势：ReLU 不是零中心的。同时，它有一个“死亡 ReLU”问题，即如果一个神经元的输入恒为负，那么它的梯度将永远是 0，这个神经元就再也无法被激活。

Tanh 的优势在于其平滑性和零中心特性，但计算成本更高，且存在梯度饱和问题。ReLU 则以其简单、高效和避免梯度消失（在正区间）的特点成为大多数现代网络的首选。

什么时候该用 Tanh？

尽管 ReLU 在很多场景下表现出色，Tanh 仍然有其不可替代的用武之地。

循环神经网络 (RNNs)：在像 LSTMs 和 GRUs 这样的循环网络中，Tanh 是隐藏层状态的默认激活函数。它的 [-1, 1] 输出范围非常适合控制信息流的门控机制，并保持网络内部状态的稳定，防止信息在时间步之间爆炸或消失得太快。
需要有界输出的场景：如果你的模型输出需要被限制在一个特定范围内，比如 [-1, 1]，Tanh 可以直接用在输出层。
当零中心特性很重要时：在一些对数据分布敏感的较浅网络中，Tanh 的零中心特性可以带来比 ReLU 更快的收敛和更好的性能。

总的来说，在非常深的前馈网络中，ReLU 及其变体（如 Leaky ReLU、GELU）通常是更好的选择。但在 RNNs 和一些特定架构中，Tanh 依然是标准配置。

在 PyTorch 中使用 Tanh

在 PyTorch 中使用 Tanh 非常简单，可以直接作为 torch.nn 模块的一个层，也可以直接作为函数调用。

import torch
import torch.nn as nn

# 1. 作为模型的一层
model = nn.Sequential(
    nn.Linear(10, 20),
    nn.Tanh(),  # 将 Tanh 作为激活层
    nn.Linear(20, 1)
)

input_tensor = torch.randn(5, 10)
output = model(input_tensor)
print("模型输出:\n", output)

# 2. 直接作为函数调用
x = torch.tensor([-2.0, -1.0, 0.0, 1.0, 2.0])
tanh_output = torch.tanh(x)
print("\n函数直接调用输出:\n", tanh_output)

输出结果：

模型输出:
 tensor([[ 0.1704],
        [-0.4137],
        [ 0.1340],
        [-0.2017],
        [-0.0194]], grad_fn=<AddmmBackward0>)

函数直接调用输出:
 tensor([-0.9640, -0.7616,  0.0000,  0.7616,  0.9640])

可以看到，输出结果是对称分布在 0 两侧的，这正是 Tanh 零中心特性的体现。

结语

Tanh 函数介于 Sigmoid 的简单性和 ReLU 的高效性之间。它平滑、对称，并且在深度学习领域，尤其是在需要平衡激活值的场景下，仍然扮演着重要角色。

虽然它不再是大多数现代卷积网络架构的默认选择，但理解 Tanh 的核心优势——零中心输出——对于我们选择合适的激活函数至关重要。

最后给一个简单的经验法则：

构建大型、深层的前馈网络时，优先考虑 ReLU 及其变体。
当你需要稳定性、对称性以及更平滑的梯度流时，尤其是在 RNNs 中，Tanh 是一个非常可靠的选择。

最好的方法还是通过实验来检验，让数据告诉你哪种激活函数最适合你的任务。

关于

关注我获取更多资讯

📢 公众号

💬 个人号