从零到一，彻底搞懂离散概率分布

在数据科学和机器学习的日常工作中，我们总会遇到各种不确定性。比如网站的点击次数、一批产品里的次品数、或者客服中心一小时内接到的电话数。这些场景有个共同点：它们的结果都是可以数的整数。离散概率分布，就是我们用来描述和量化这类“可数”事件不确定性的核心工具。

你可能听说过 Netflix 用它来做推荐，银行用它来评估信贷风险，工厂用它来做质检。没错，这些分布远不止是课本里的数学公式，它们是解决现实问题的基本模块。

这篇文章，我会带你把离散概率分布彻底搞懂。咱们不仅会聊聊理论，更会上手 Python 代码，看看这些分布在实际中到底是怎么用的。

什么是离散概率分布？

说白了，离散概率分布就是给一堆可数的结果，分别赋予一个概率。这些结果可以是 0, 1, 2, 3... 这样的数字，也可以是“红、蓝、绿”这样的分类。

一个合法的离散概率分布，必须遵守两条铁律：

所有结果的概率都必须大于等于 0。负数概率没意义，这很直观。
所有结果的概率加起来必须等于 1。这保证了所有可能性都被我们考虑到了。

最经典的例子就是扔一个公平的六面骰子。每个点数出现的概率都是 1/6，这六个概率加起来正好是 1。

搞清楚这个，我们就能回答很多实际问题，比如：

扔 5 次硬币，恰好出现 3 次正面的概率是多大？
一个生产线上，抽检 100 个零件，我们预期会发现多少个次品？
今天进店的顾客里，至少有一人下单的概率是多少？

这些问题都直接关系到业务指标和风险评估，所以说，掌握它们很有必要。

离散 vs. 连续，有啥不一样？

这俩最根本的区别在于处理的数据类型：

离散分布处理的是计数，比如客户数、点击数。我们关心的是某个精确值发生的概率，比如 P(X=2)，即“恰好来了2个客户的概率”。
连续分布处理的是测量，比如身高、体重、时间。我们不关心某个精确值的概率（理论上是0），而是关心一个区间的概率，比如 P(160 <= 身高 <= 170)。

从图形上看，离散分布像一个条形图（或者叫阶梯函数），每个“柱子”代表一个计数值的概率。而连续分布则是一条平滑的曲线，比如大家熟知的正态分布“钟形曲线”。

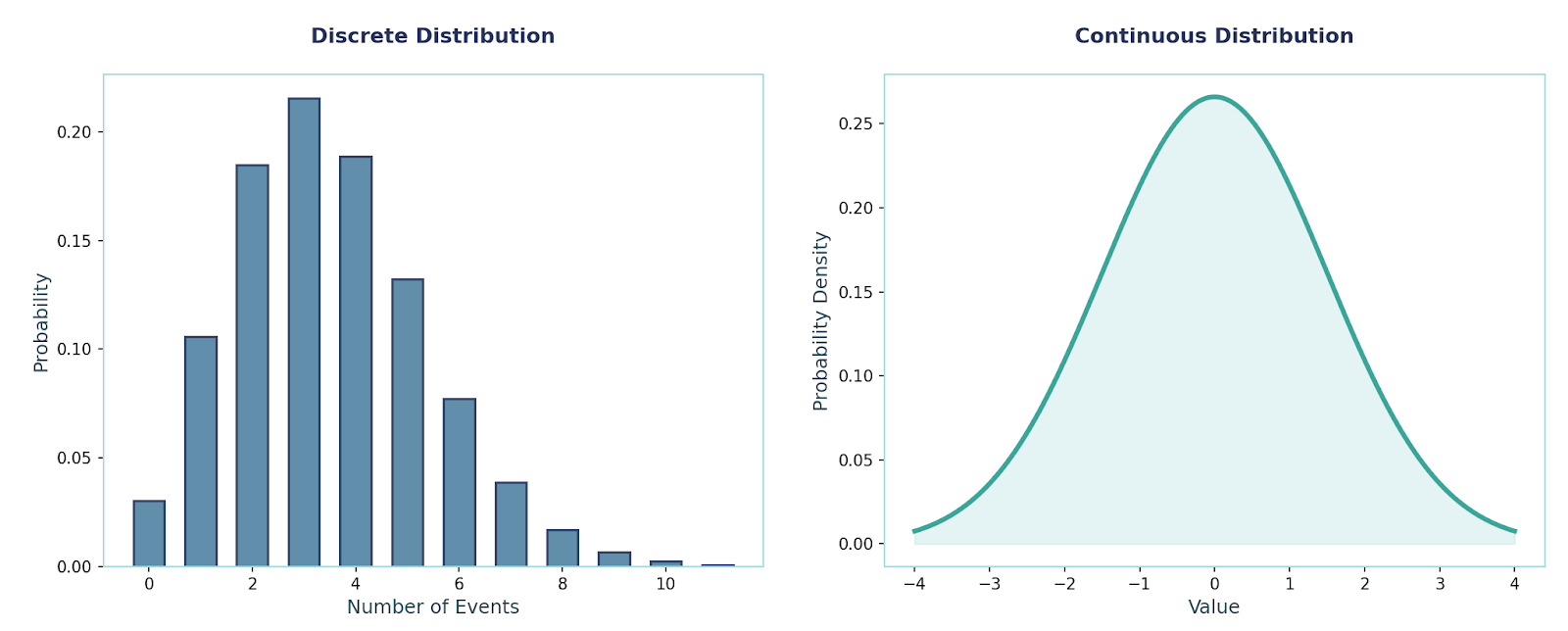
离散分布与连续分布的对比图

选择哪个，就看你的数据是数的，还是量的。

理解分布的数学工具箱

在深入各种具体的分布之前，我们得先熟悉几个基本工具。这些概念是理解和使用所有概率分布的基础。

概率质量函数 (PMF)

PMF (Probability Mass Function) 是离散分布的核心。它直接告诉我们，随机变量取某个精确值的概率是多少，记作 p(x) = P(X=x)。我们前面说的那两条铁律，就是对 PMF 的约束。

PMF 非常有用，有了它我们就能计算分布的各种统计特性，比如均值和方差。

举个例子，假设一个随机变量 X 的取值和概率如下： p(0)=0.1, p(1)=0.2, p(2)=0.3, p(3)=0.4

均值 (期望值): E[X] = 0*(0.1) + 1*(0.2) + 2*(0.3) + 3*(0.4) = 2.0
二阶矩: E[X²] = 0²*(0.1) + 1²*(0.2) + 2²*(0.3) + 3²*(0.4) = 5.0
方差: Var(X) = E[X²] - (E[X])² = 5.0 - 2.0² = 1.0

累积分布函数 (CDF)

CDF (Cumulative Distribution Function) 回答的是“随机变量小于或等于某个值的概率是多少”，记作 F(x) = P(X ≤ x)。它的的得意义在于累加，把所有小于等于 x 的值的概率都加起来。

对于离散分布，CDF 是一系列阶梯状的跳跃。

继续用上面的例子：

F(0) = P(X ≤ 0) = 0.1
F(1) = P(X ≤ 1) = p(0) + p(1) = 0.1 + 0.2 = 0.3
F(2) = P(X ≤ 2) = p(0) + p(1) + p(2) = 0.1 + 0.2 + 0.3 = 0.6
F(3) = P(X ≤ 3) = 1.0

矩和矩生成函数 (MGF)

“矩” (Moment) 是用来描述分布形状的数字。

一阶矩就是均值，描述分布的中心位置。
二阶中心矩是方差，描述分布的离散程度。
三阶中心矩关联到偏度 (Skewness)，描述分布是否对称。
四阶中心矩关联到峰度 (Kurtosis)，描述分布的尾部厚重程度或峰值尖锐程度。

而矩生成函数 (Moment Generating Function, MGF) 是一个更高级的工具，可以把它看作一个能“生成”所有矩的函数。它的定义是 M(t) = E[e^(tX)]。通过对 MGF 求导再取 t=0，就能轻松得到各阶矩，非常方便。

常见离散分布逐个看

好了，理论工具准备好了，我们来看看几个在实践中最常用的离散分布。

伯努利分布 (Bernoulli Distribution)

这是最简单的分布，没有之一。它描述的是一次实验，结果只有两种：成功 (1) 或失败 (0)。

应用场景：任何单次的二元事件，比如一次点击是否转化、一封邮件是否被打开、一个零件是否合格。
PMF: P(X=x) = pˣ(1-p)¹⁻ˣ，其中 x 只能是 0 或 1，p 是成功的概率。
均值: p
方差: p(1-p)

Python 示例:

from scipy.stats import bernoulli

p = 0.6 # 成功的概率
rv = bernoulli(p)

# 计算成功（X=1）和失败（X=0）的概率
print(f"P(X=1) = {rv.pmf(1)}")
print(f"P(X=0) = {rv.pmf(0)}")

二项分布 (Binomial Distribution)

二项分布是伯努利分布的升级版。它描述的是进行 n 次独立的伯努利实验，成功的概率始终为 p，我们想知道总共成功了多少次。

三大假设：固定的试验次数 n、各次试验相互独立、每次试验成功概率 p 相同。
应用场景：A/B 测试中 n 个用户有多少人点击、质检中抽查 n 个产品有多少个次品。
PMF: P(X=x) = C(n, x) * pˣ * (1-p)ⁿ⁻ˣ
均值: np
方差: np(1-p)

Python 示例:

from scipy.stats import binom

n, p = 10, 0.3 # 10次试验，每次成功概率0.3
x = 4          # 恰好成功4次

rv = binom(n, p)
print(f"P(X=4) = {rv.pmf(x):.4f}") # 输出约为 0.2001

几何分布 (Geometric Distribution)

几何分布关心的是，在成功的概率为 p 的伯努利实验中，第一次成功需要尝试多少次。

核心特性：无记忆性。意思是过去的失败不影响未来的成功概率。比如，你已经扔了5次硬币都是反面，下一次扔出正面的概率依然是0.5，不会因为你“倒霉”了很久而改变。
应用场景：需要多少次点击才能获得第一个转化？试多少次才能让代码跑通？
PMF: P(X=k) = (1-p)ᵏ⁻¹ * p
均值: 1/p
方差: (1-p)/p²

Python 示例:

from scipy.stats import geom

p, k = 0.2, 3 # 成功概率0.2，问第3次才成功的概率
rv = geom(p)
print(f"P(X=3) = {rv.pmf(k):.4f}") # 输出为 0.128

泊松分布 (Poisson Distribution)

泊松分布用来描述在一个固定的时间或空间间隔内，独立事件发生的次数。这些事件的平均发生率是固定的，用 λ (lambda) 表示。

应用场景：一小时内网站服务器收到的请求数、一本书每页的错别字数、一个路口一分钟内通过的车辆数。它很适和模拟那些“稀有但平稳”的事件。
PMF: P(X=x) = (e⁻ˡ * λˣ) / x!
均值: λ
方差: λ (没错，它的均值和方差相等，这是一个很有趣的特性)

Python 示例:

from scipy.stats import poisson

lam = 3 # 平均每小时接到3个电话
rv = poisson(mu=lam)

# 计算一小时内一个电话都没接到的概率
print(f"P(X=0) = {rv.pmf(0):.4f}") # 输出约为 0.0498

结语

离散概率分布是数据科学工具箱里的基石。它们为我们理解和建模那些可数的、随机的现象提供了一套强大的语言。

从简单的伯努利分布到更复杂的负二项分布，每一种都有其独特的“故事”和适用场景。掌握它们，意味着你不仅能看懂数据，还能洞察数据背后的规律和不确定性。希望这篇文章能帮你把这块知识拼图拼得更完整。

关于

关注我获取更多资讯

📢 公众号

💬 个人号